Plot a turbine in 3D using Python
The samples presented in this article are a series of functions and scripts that will plot a turbine assembly and it's components in 3D. The component scripts will work with any of the following components:
- Tower:
plot_tower.py - Hub:
plot_hub.py - Drivetrain and Nacelle:
plot_drivetrain_and_nacelle.py - Blade:
plot_blade.py
The final sample connects (plot_assembly.py) all the components and plots in a full 3D turbine assembly.
The scripts in their supplied form plot the IEA 15MW turbine (NG_IEA_15_Onshore_SteadyOP.json). They can be used with other turbines, but they need to have the same components and the same structure. For different structures and extra components the user will have to change the files themselves.
Prerequisites
- Latest version of Bladed Next Gen and Samples installed including the Bladed Python packages.
- Licence for Bladed Next Gen (request a licence).
- Python 3.9 to 3.12 installed.
What you will learn
- Identifying the JSON input file geometry properties and what they mean in a 3D space.
How to use this tutorial
To use this tutorial it is advised to download the samples. The package contains all required content to complete this tutorial.
Make sure to check the Get started article on how to setup your machine for the tutorials.
Switch to the samples folder and run each of the Python scripts described in this article.
Plot a tower
"""
plot_tower.py
This example script demonstrates how to plot the Tower component of the provided NG_IEA_15_Onshore_SteadyOP turbine model.
It showcases how to extract input data and visualize it using 3D plots.
Please note that this script is specific to the NG_IEA_15_Onshore_SteadyOP model and may not be compatible with other turbine models.
Requirements:
- tower_plot.py
- dnv_bladed_models (imported as models)
- numpy
- matplotlib
Usage:
1. Ensure that the required components (tower_plot.py, dnv_bladed_models) are available.
2. Make sure the required files and the NG_IEA_15_Onshore_SteadyOP.json are in the same folder.
3. Run the script to visualize the Tower component in a 3D plot.
"""
import os
import dnv_bladed_models as models
import matplotlib.pyplot as plt
import numpy as np
def plot_tower(figure_axis, tower):
# Plots a tower structure using 3D surface plots for each can section.
# Extract information from the Tower object
can_list = tower.Cans
first_can = True
tower_height = 0
# Iterate through each can in the list
for i_can, can in enumerate(can_list):
can_height = can.CanHeight
# Calculate starting point and previous height
if first_can:
first_can = False
can_starting_point = 0
previous_height = can_height
else:
can_starting_point = previous_height
previous_height = can_starting_point + can_height
# Calculate base and top radii
base_outer_radius = can.BaseSection.OutsideDiameter / 2
base_inner_radius = can.BaseSection.OutsideDiameter / 2 - can_list[0].BaseSection.WallThickness
if hasattr(can_list[0], 'TopSection'):
if not can_list[0].TopSection is None:
top_outer_radius = can.TopSection.OutsideDiameter / 2
top_inner_radius = can.TopSection.OutsideDiameter / 2 - can_list[0].TopSection.WallThickness
else:
top_outer_radius = base_outer_radius
top_inner_radius = base_inner_radius
else:
top_outer_radius = base_outer_radius
top_inner_radius = base_inner_radius
tower_height = tower_height + can.CanHeight
# Plot surfaces for outer and inner radii
x_grid, y_grid, z_grid = can_surface(base_outer_radius, top_outer_radius, can_starting_point, can_height)
figure_axis.plot_surface(x_grid, y_grid, z_grid, alpha=0.5, color='grey')
figure_axis.text(x_grid[0][0], y_grid[0][0], z_grid[0][0], 'Can '+str(i_can))
x_grid, y_grid, z_grid = can_surface( base_inner_radius, top_inner_radius, can_starting_point, can_height)
figure_axis.plot_surface(x_grid, y_grid, z_grid, alpha=0.5, color='k')
# Set plot limits
x_max = max(x_grid.max(), y_grid.max(), z_grid.max())
plt.xlim([-x_max / 2, x_max / 2])
plt.ylim([-x_max / 2, x_max / 2])
figure_axis.set_zlim(0, x_max)
# Plot assembly nodes
figure_axis.scatter3D(0, 0, 0, marker='v', color="green")
assembly_node = np.array([0, 0, tower_height])
figure_axis.scatter3D(assembly_node[0], assembly_node[1], assembly_node[2], marker='^', color="green")
return assembly_node
def can_surface(base_radius, top_radius, can_starting_point, can_height):
# Generates a 3D surface representation of a truncated cone (can) using parametric equations
# Create an array of z values along the height of the can
z = np.linspace(can_starting_point, can_starting_point+can_height, 5)
# Create an array of theta values (angle around the z-axis)
theta = np.linspace(0, 2*np.pi, 50)
# Create a grid of theta and z values
theta_grid, z_grid = np.meshgrid(theta, z)
# Calculate the varying radius along the height
radius = base_radius + (top_radius - base_radius) * z_grid / can_height
# Calculate x and y coordinates using polar coordinates
x_grid = radius*np.cos(theta_grid)
y_grid = radius*np.sin(theta_grid)
return x_grid, y_grid, z_grid
if __name__ == "__main__":
# Specify required folders, relative to this script
examples_models_path = os.path.dirname(__file__)
# read in a full analysis from file
analysis_model_file_path = os.path.join(examples_models_path, 'NG_IEA_15_Onshore_SteadyOP.json')
# Extract the components of the project file
Components = models.BladedAnalysis.from_file(analysis_model_file_path).ComponentDefinitions
# Figure settings
fig, figure_axis = plt.subplots(subplot_kw={"projection": "3d"}, figsize=(15, 10))
figure_axis.set(xlabel='X-axis', ylabel='Y-axis', zlabel='Z-axis')
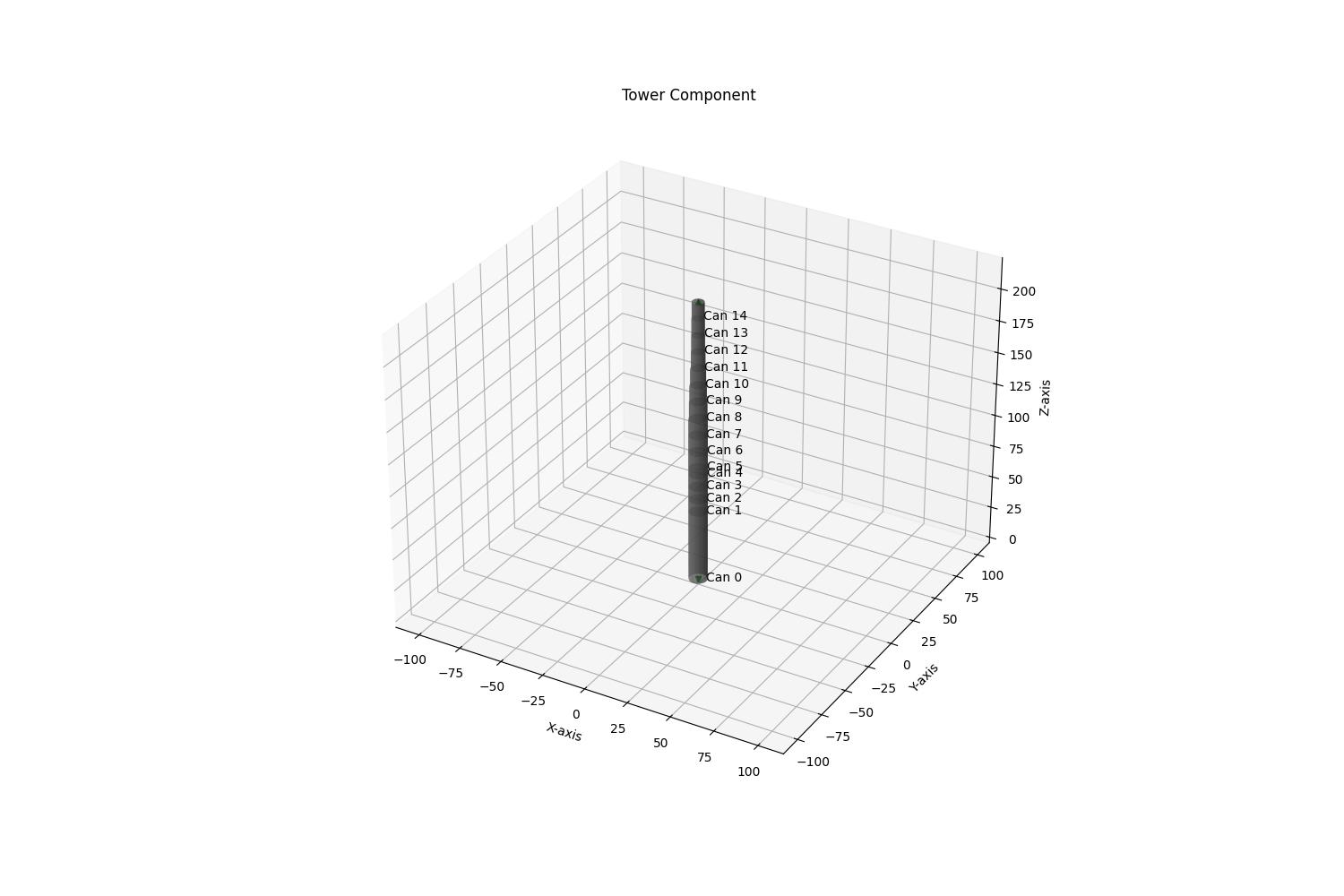
figure_axis.set_title("Tower Component")
# Plots the tower
plot_tower(figure_axis, Components['IEA15Tower'])
plt.show()
Plot a nacelle and drivetrain
"""
plot_drivetrain_and_nacelle.py
This example script demonstrates how to plot the DrivetrainAndNacelle component of the provided NG_IEA_15_Onshore_SteadyOP turbine model.
It showcases how to extract input data and visualize it using 3D plots.
Please note that this script is specific to the NG_IEA_15_Onshore_SteadyOP model and may not be compatible with other turbine models.
Requirements:
- drivetrain_and_nacelle_plot.py
- dnv_bladed_models (imported as models)
- numpy
- scipy
- matplotlib
Usage:
1. Ensure that the required components (drivetrain_and_nacelle_plot.py, dnv_bladed_models) are available.
2. Make sure the required files and the NG_IEA_15_Onshore_SteadyOP.json are in the same folder.
3. Run the script to visualize the DrivetrainAndNacelle component in a 3D plot.
"""
import os
import dnv_bladed_models as models
import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial.transform import Rotation as R
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
def create_box_points_and_faces(centre, length, width, height, initial_coordinates):
# Creates points and faces for a 3D box (cuboid) given its center, dimensions, and initial coordinates.
half_length = length / 2
half_width = width / 2
half_height = height / 2
# Define the 8 corner points of the box
points = np.array([
[centre[0] - half_length, centre[1] - half_width, centre[2] - half_height],
[centre[0] + half_length, centre[1] - half_width, centre[2] - half_height],
[centre[0] + half_length, centre[1] + half_width, centre[2] - half_height],
[centre[0] - half_length, centre[1] + half_width, centre[2] - half_height],
[centre[0] - half_length, centre[1] - half_width, centre[2] + half_height],
[centre[0] + half_length, centre[1] - half_width, centre[2] + half_height],
[centre[0] + half_length, centre[1] + half_width, centre[2] + half_height],
[centre[0] - half_length, centre[1] + half_width, centre[2] + half_height]
]) + initial_coordinates
# Define the faces of the box (each face as a list of points)
faces = [[points[0], points[1], points[2], points[3]],
[points[4], points[5], points[6], points[7]],
[points[0], points[1], points[5], points[4]],
[points[2], points[3], points[7], points[6]],
[points[1], points[2], points[6], points[5]],
[points[4], points[7], points[3], points[0]]]
return points, faces
def plot_nacelle(figure_axis, drivetrain_and_nacelle, initial_coordinates=np.array([0.0, 0.0, 0.0])):
# PLots the nacelle assembly in 3D space
# Specify dimensions (width, length, height)
width = drivetrain_and_nacelle.NacelleCover.Width
length = drivetrain_and_nacelle.NacelleCover.Length
height = drivetrain_and_nacelle.NacelleCover.Height
# Specify the centre point (x, y, z). Assumes the geometric centre coincides with the centre of pressure.
centre = (drivetrain_and_nacelle.NacelleCover.CentreOfPressure.X,
drivetrain_and_nacelle.NacelleCover.CentreOfPressure.Y,
drivetrain_and_nacelle.NacelleCover.CentreOfPressure.Z) # centre position (x, y, z)
# Specify hub assembly point and direction
hub_assembly_point = np.zeros(3)
hub_assembly_point[0] = - drivetrain_and_nacelle.PositionOfHubCentre.Overhang
hub_assembly_point[1] = drivetrain_and_nacelle.PositionOfHubCentre.SideOffset
hub_assembly_point[2] = drivetrain_and_nacelle.PositionOfHubCentre.HeightOffset
# Tilt rotation matrix
hub_assembly_tilt = R.from_euler('y', drivetrain_and_nacelle.PositionOfHubCentre.RotorTilt).as_matrix()
# Compute the eight corner points (vertices) and faces
points, faces = create_box_points_and_faces(centre, length, width, height, initial_coordinates)
# Plot the parallelepiped
figure_axis.scatter3D(*points.T, color='red', alpha=0) # Plot vertices
# Plot the faces
figure_axis.add_collection3d(Poly3DCollection(faces, facecolors='grey', linewidths=1, edgecolors='black', alpha=0.25))
# Plot previous assembly point
figure_axis.scatter3D(*initial_coordinates, color='g', marker='v')
# Rotate hub pitch:
shaft_unit_vector = hub_assembly_tilt.dot(np.array([1.0, 0.0, 0.0]))
# Start location of the low speed shaft
shaft_start = np.array([0.0, 0.0, 0.0])
shaft_start[0] = hub_assembly_point[0] + (length/2-hub_assembly_point[0]) * shaft_unit_vector[0]
shaft_start[1] = hub_assembly_point[1]
shaft_start[2] = hub_assembly_point[2] + (length/2-hub_assembly_point[0]) * shaft_unit_vector[2]
# Rotate as to horizontal of nacelle:
shaft_start = shaft_start + initial_coordinates
# Rotate assembly
hub_assembly_point = hub_assembly_point + initial_coordinates
# Plot next assembly point
figure_axis.scatter3D(hub_assembly_point[0], hub_assembly_point[1], hub_assembly_point[2], color='g', marker='^')
figure_axis.text(hub_assembly_point[0], hub_assembly_point[1], hub_assembly_point[2], 'Position Of Hub Centre')
# Nacelle mid point
midpoint = np.average(points, axis=0)
figure_axis.text(midpoint[0], midpoint[1], midpoint[2], 'Nacelle')
# Plot shaft
figure_axis.plot([hub_assembly_point[0], shaft_start[0]], [hub_assembly_point[1], shaft_start[1]], zs=[hub_assembly_point[2], shaft_start[2]])
plt.xlim([min(hub_assembly_point[0], initial_coordinates[1]-width/2, initial_coordinates[2]-height),
max(initial_coordinates[0]+length/2, initial_coordinates[1]+width/2, initial_coordinates[2]+height)])
plt.ylim([min(hub_assembly_point[0], initial_coordinates[1]-width/2, initial_coordinates[2]-height),
max(initial_coordinates[0]+length/2, initial_coordinates[1]+width/2, initial_coordinates[2]+height)])
figure_axis.set_zlim(min(hub_assembly_point[0], initial_coordinates[1]-width/2, initial_coordinates[2]-height), max(
initial_coordinates[0]+length/2, initial_coordinates[1]+width/2, initial_coordinates[2]+height))
return hub_assembly_point, hub_assembly_tilt
if __name__ == "__main__":
# Specify required folders, relative to this script
examples_models_path = os.path.dirname(__file__)
# Read in a full analysis from file
analysis_model_file_path = os.path.join(examples_models_path, 'NG_IEA_15_Onshore_SteadyOP.json')
# Extract the components of the project file
Components = models.BladedAnalysis.from_file(analysis_model_file_path).ComponentDefinitions
# Figure settings
fig, figure_axis = plt.subplots(subplot_kw={"projection": "3d"}, figsize=(15, 10))
figure_axis.set(xlabel='X-axis', ylabel='Y-axis', zlabel='Z-axis')
figure_axis.set_title("DrivetrainAndNacelle Component")
# Plots the nacelle and drivetrain low speed shaft
plot_nacelle(figure_axis, Components['IEA15DrivetrainAndNacelle'])
plt.show()

Plot a blade hub
"""
plot_hub.py
This example script demonstrates how to plot the Hub component of the provided NG_IEA_15_Onshore_SteadyOP turbine model.
It showcases how to extract input data and visualize it using 3D plots.
Please note that this script is specific to the NG_IEA_15_Onshore_SteadyOP model and may not be compatible with other turbine models.
Requirements:
- hub_plot.py
- dnv_bladed_models (imported as models)
- numpy
- scipy
- matplotlib
Usage:
1. Ensure that the required components (hub_plot.py, dnv_bladed_models) are available.
2. Make sure the required files and the NG_IEA_15_Onshore_SteadyOP.json are in the same folder.
3. Run the script to visualize the Hub component in a 3D plot.
"""
import os
import dnv_bladed_models as models
import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial.transform import Rotation as R
def plot_hub(figure_axis, hub, rotor_tilt=np.eye(3), initial_coordinates=np.array([0.0, 0.0, 0.0])):
# Plots the hub and calculates the blade mounting points
# Radius of the hub
hub_radius = hub.Spinner.Diameter/2
# Plot the hub as a sphere
plot_half_sphere(figure_axis, hub_radius, initial_coordinates)
blade_rotations = []
blade_starting_points = []
azimuth_step = 2*np.pi/hub.NumberOfBlades
for i in range(0, hub.NumberOfBlades):
# Calculates the blade mounting rotations, direction and the starting points
# Calculate the rotation matrix to rotate due to different azimuth positions and coning rotation
rot_azimuth = R.from_euler('x', azimuth_step*i).as_matrix()
rot_cone = R.from_euler('y', - hub.MountingPoints.ConingAngle).as_matrix()
# Final rotation matrix due to tilt, azimuth and coning angle
blade_rotations.append(rotor_tilt.dot(rot_azimuth.dot(rot_cone)))
blade_directions = blade_rotations[i].dot(np.array([0.0, 0.0, 1.0]))
blade_starting_points.append(initial_coordinates + blade_directions * hub.MountingPoints.RadiusOfBladeConnection)
# Plot blade connections
figure_axis.plot([initial_coordinates[0], blade_starting_points[i][0]], [
initial_coordinates[1], blade_starting_points[i][1]], zs=[initial_coordinates[2], blade_starting_points[i][2]])
# Plot blade starting points
figure_axis.scatter3D(blade_starting_points[i][0], blade_starting_points[i][1], blade_starting_points[i][2], color='g', marker='^')
# Plot hub center
figure_axis.scatter3D(initial_coordinates[0], initial_coordinates[1], initial_coordinates[2], color='g', marker='v')
return blade_starting_points, blade_rotations
def plot_half_sphere(figure_axis, radius, initial_coordinates):
# Define the number of steps
step = np.pi/10
# Define the co-ordinates of points in the sphere
phi = np.arange(0 , np.pi + step, step) # Only half of a shpere
theta = np.arange(np.pi / 2, np.pi * 1.5 + step, step)
phi, theta = np.meshgrid(phi, theta)
# Convert spherical coordinates to cartesian coordinates
x = radius * np.sin(phi) * np.cos(theta) + initial_coordinates[0]
y = radius * np.sin(phi) * np.sin(theta) + initial_coordinates[1]
z = radius * np.cos(phi) + initial_coordinates[2]
# Create a 3D plot
figure_axis.plot_surface(x, y, z, color='grey', alpha=0.5)
if __name__ == "__main__":
# Specify required folders, relative to this script
examples_models_path = os.path.dirname(__file__)
# Read in a full analysis from file
analysis_model_file_path = os.path.join(examples_models_path, 'NG_IEA_15_Onshore_SteadyOP.json')
# Extract the components of the project file
Components = models.BladedAnalysis.from_file(analysis_model_file_path).ComponentDefinitions
# Figure settings
fig, figure_axis = plt.subplots(subplot_kw={"projection": "3d"}, figsize=(15, 10))
figure_axis.set(xlabel='X-axis', ylabel='Y-axis', zlabel='Z-axis')
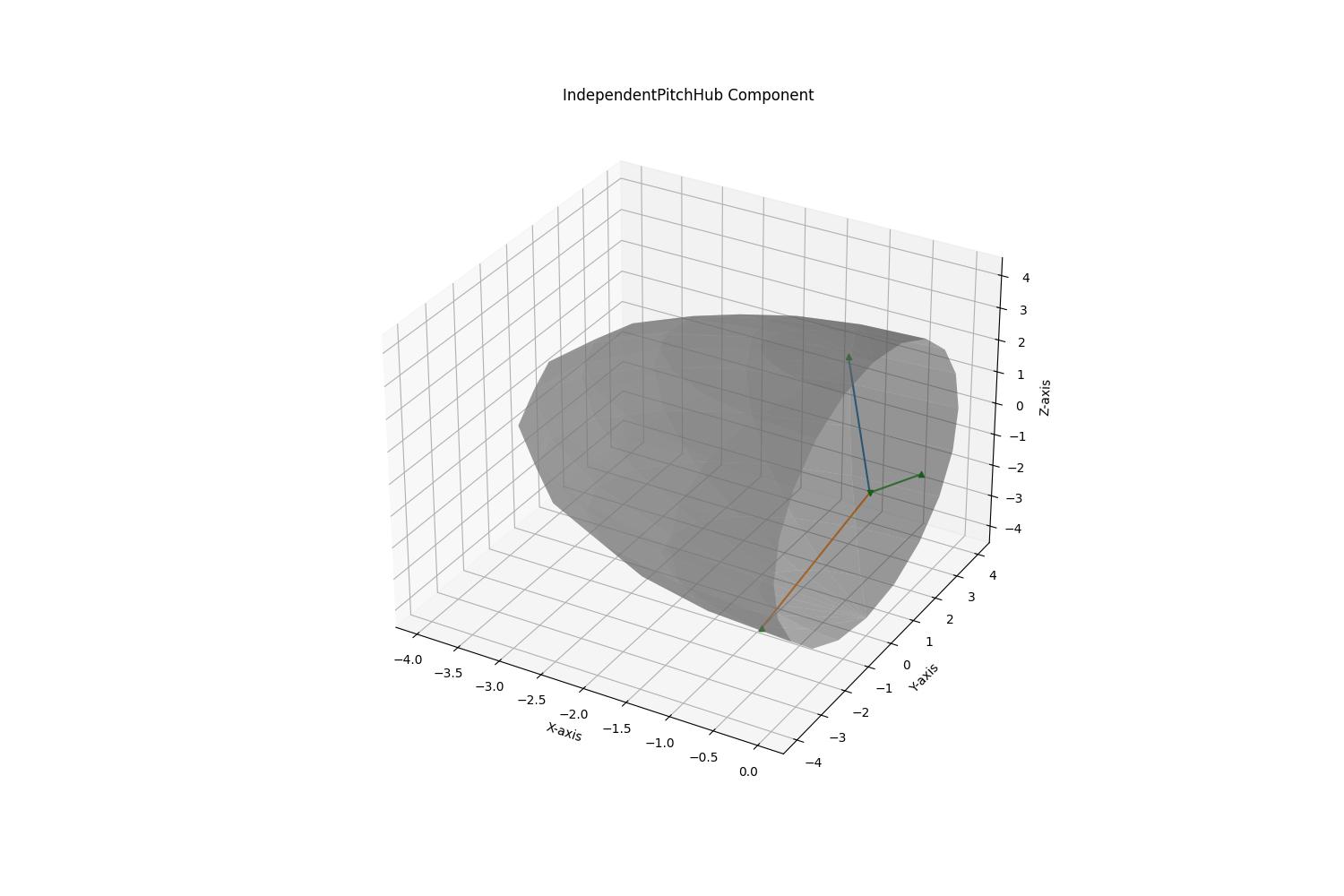
figure_axis.set_title("IndependentPitchHub Component")
plot_hub(figure_axis, Components['IEA15Hub'])
plt.show()
Plot a blade
"""
plot_blade.py
This example script demonstrates how to plot the Blade component of the provided NG_IEA_15_Onshore_SteadyOP turbine model.
It showcases how to extract input data and visualize it using 3D plots.
Please note that this script is specific to the NG_IEA_15_Onshore_SteadyOP model and may not be compatible with other turbine models.
Requirements:
- blade_plot.py
- dnv_bladed_models (imported as models)
- numpy
- scipy
Usage:
1. Ensure that the required components (blade_plot.py, dnv_bladed_models) are available.
2. Make sure the required files and the NG_IEA_15_Onshore_SteadyOP.json are in the same folder.
3. Run the script to visualize the Blade component in a 3D plot.
"""
import os
import numpy as np
import matplotlib.pyplot as plt
import dnv_bladed_models as models
from scipy.spatial.transform import Rotation as R
def plot_blade(figure_axis, blade, initial_coordinates=np.array([0, 0, 0]), blade_rotations=np.eye(3)):
# Plots the blade given the blade data, initial coordinates and blade mounting angles
# Transformations are based on the theory presented in the Bladed Next Gen Online Documentation: "Blade Coordinate Systems Theory"
reference_systems = np.empty((0, 3))
leading_edges = np.empty((0, 3))
trailing_edges = np.empty((0, 3))
quarter_chords = np.empty((0, 3))
for blade_section in blade.SectionDefinitions:
# Extract relevant data from blade section
coordinate_system = blade_section.AxesAndCoordinateSystems
blade_reference_axis = coordinate_system.ReferenceCoordinateSystem
blade_aerodynamic_properties = blade_section.AerodynamicProperties
blade_quarter_chord_axis = coordinate_system.QuarterChordCoordinateSystem
# Extracts the unit vectors of the reference coordinate system
unit_z_axis = np.array([blade_reference_axis.ZAxis.X, blade_reference_axis.ZAxis.Y, blade_reference_axis.ZAxis.Z])
unit_y_axis = np.array([blade_reference_axis.YAxis.X, blade_reference_axis.YAxis.Y, blade_reference_axis.YAxis.Z])
unit_x_axis = (np.cross(unit_y_axis, unit_z_axis)) / np.linalg.norm(np.cross(unit_y_axis, unit_z_axis))
# Extract origin and rotation matrix from the blade root cordinate system to the reference coordinate system
o_root_ref = np.array([blade_reference_axis.Origin.X, blade_reference_axis.Origin.Y, blade_reference_axis.Origin.Z])
rotation_root_ref = np.column_stack((unit_x_axis, unit_y_axis, unit_z_axis))
# Extract origin and rotation matrix from the blade reference cordinate system to the quarter chord coordinate system
rotation_ref_quarter = R.from_euler('z', blade_quarter_chord_axis.RotationAboutReferenceZ).as_matrix()
o_ref_quarter = np.array([blade_quarter_chord_axis.OffsetInReferenceX, blade_quarter_chord_axis.OffsetInReferenceY, 0.0])
# Combines them into a rotation and translation from the root coordinate system to the quarter chord coordinate system
rotation_root_quarter = rotation_root_ref.dot(rotation_ref_quarter)
o_root_quarter = o_root_ref + rotation_root_ref.dot(o_ref_quarter)
# Creates the transformation matrix for the QuarterChordCoordinateSystem
f_qc = np.column_stack((rotation_root_quarter, o_root_quarter))
f_qc = np.vstack((f_qc, np.array([0, 0, 0, 1])))
# Uses the transformation matrix to calculate the location of the leading and trailing edge
leading_edge_location = f_qc.dot(np.array([0, -0.25*blade_aerodynamic_properties.Chord, 0, 1]))[0:3]
trailing_edge_location = f_qc.dot(np.array([0, 0.75*blade_aerodynamic_properties.Chord, 0, 1]))[0:3]
quarter_chord_location = f_qc[0:3, 3]
# Rotates the locations to account for the different azimuth positions and adds the initial positions to get them into global coordinates
quarter_chord_location = blade_rotations.dot(quarter_chord_location) + initial_coordinates
leading_edge_location = blade_rotations.dot(leading_edge_location) + initial_coordinates
trailing_edge_location = blade_rotations.dot(trailing_edge_location) + initial_coordinates
reference_system_location = blade_rotations.dot(o_root_ref) + initial_coordinates
quarter_chords = np.vstack((quarter_chords, quarter_chord_location))
leading_edges = np.vstack((leading_edges, leading_edge_location))
trailing_edges = np.vstack((trailing_edges, trailing_edge_location))
reference_systems = np.vstack((reference_systems, reference_system_location))
# Plots the quarter chord location, trailing edge and the leading edge
figure_axis.scatter3D(quarter_chords[:, 0], quarter_chords[:, 1], quarter_chords[:, 2], color='b', label='Quarter Chord')
figure_axis.scatter3D(leading_edges[:, 0], leading_edges[:, 1], leading_edges[:, 2], color='r', label='Leading Edge')
figure_axis.scatter3D(trailing_edges[:, 0], trailing_edges[:, 1], trailing_edges[:, 2], color='g', label='Trailing Edge')
figure_axis.scatter3D(reference_systems[:, 0], reference_systems[:, 1], reference_systems[:, 2], color='c', label='Reference Coordinate System')
# Update maximum coordinates for plot limits
maximum = np.max(np.concatenate((quarter_chords, leading_edges, trailing_edges)))
plt.xlim([-maximum/2, maximum/2])
plt.ylim([-maximum/2, maximum/2])
figure_axis.set_zlim(0, maximum)
if __name__ == "__main__":
# Specify required folders, relative to this script
examples_models_path = os.path.dirname(__file__)
# Read in a full analysis from file
analysis_model_file_path = os.path.join(examples_models_path, 'NG_IEA_15_Onshore_SteadyOP.json')
# Extract the components of the project file
Components = models.BladedAnalysis.from_file(analysis_model_file_path).ComponentDefinitions
# Figure settings
fig, figure_axis = plt.subplots(subplot_kw={"projection": "3d"}, figsize=(15, 10))
figure_axis.set(xlabel='X-axis', ylabel='Y-axis', zlabel='Z-axis')
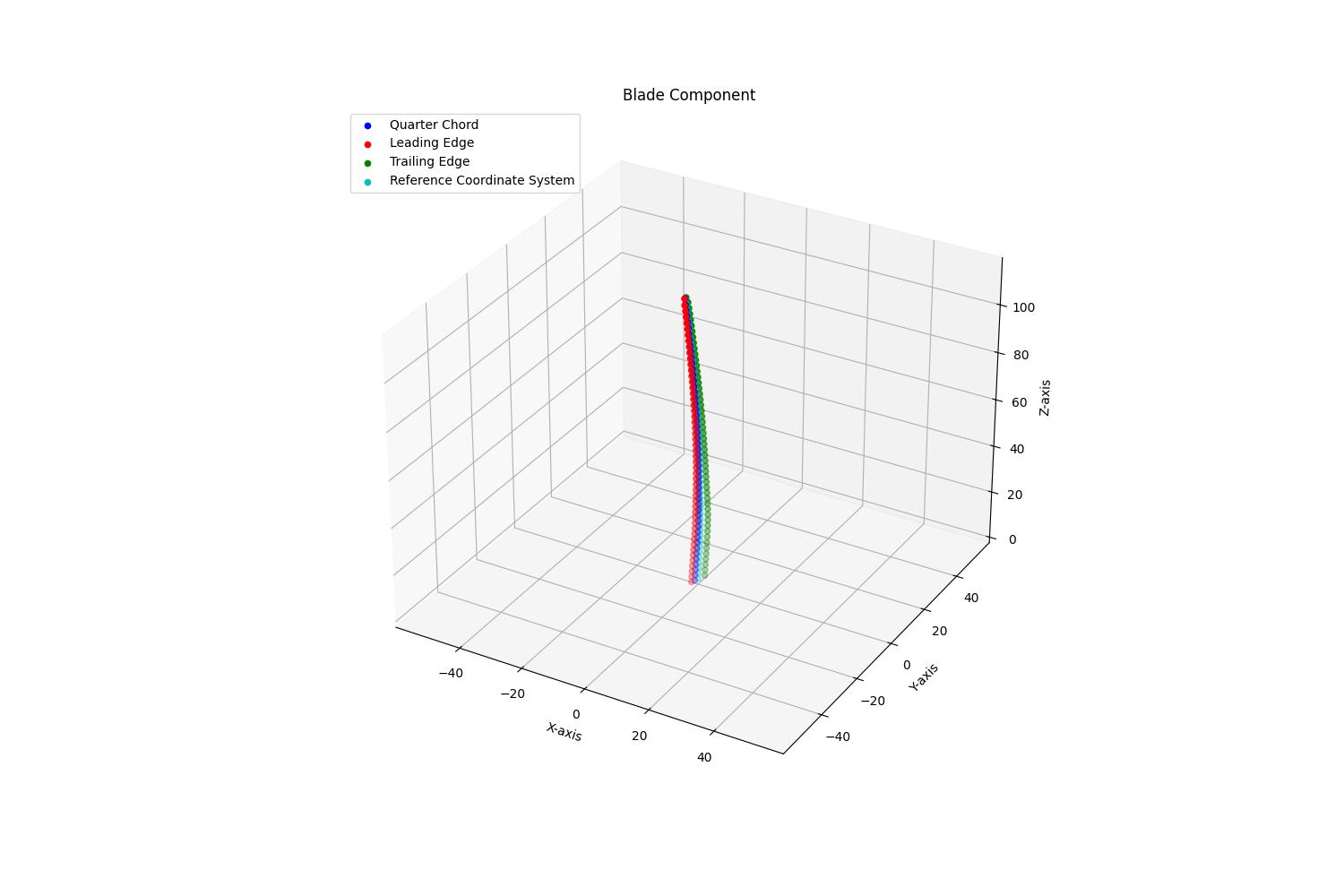
figure_axis.set_title("Blade Component")
# Plots the blade
plot_blade(figure_axis, Components['IEA15Blade'])
figure_axis.legend(loc = 'upper left')
plt.show()
Plot a turbine assembly
"""
plot_assembly.py
This example script demonstrates how to plot various components of the provided NG_IEA_15_Onshore_SteadyOP turbine model.
It showcases how to extract input data and visualize it using 3D plots.
Please note that this script is specific to the NG_IEA_15_Onshore_SteadyOP model and may not be compatible with other turbine models.
Requirements:
- blade_plot.py
- dnv_bladed_models (imported as models)
- drivetrain_and_nacelle_plot.py
- hub_plot.py
- tower_plot.py
Usage:
1. Ensure that the required components (blade_plot.py, dnv_bladed_models, drivetrain_and_nacelle_plot.py, hub_plot.py, tower_plot.py) are available.
2. Make sure the required files and the NG_IEA_15_Onshore_SteadyOP.json are in the same folder.
3. Run the script to visualize the turbine components in a 3D plot.
"""
import os
import matplotlib.pyplot as plt
import dnv_bladed_models as models
from plot_blade import plot_blade
from plot_drivetrain_and_nacelle import plot_nacelle
from plot_hub import plot_hub
from plot_tower import plot_tower
if __name__ == "__main__":
# Specify required folders, relative to this script
examples_models_path = os.path.dirname(__file__)
# Read in a full analysis from file
analysis_model_file_path = os.path.join(examples_models_path, 'NG_IEA_15_Onshore_SteadyOP.json')
# Extract the components of the project file
Components = models.BladedAnalysis.from_file(analysis_model_file_path).ComponentDefinitions
# Figure settings
fig, figure_axis = plt.subplots(subplot_kw={"projection": "3d"}, figsize=(15, 10))
figure_axis.set(xlabel='X-axis', ylabel='Y-axis', zlabel='Z-axis')
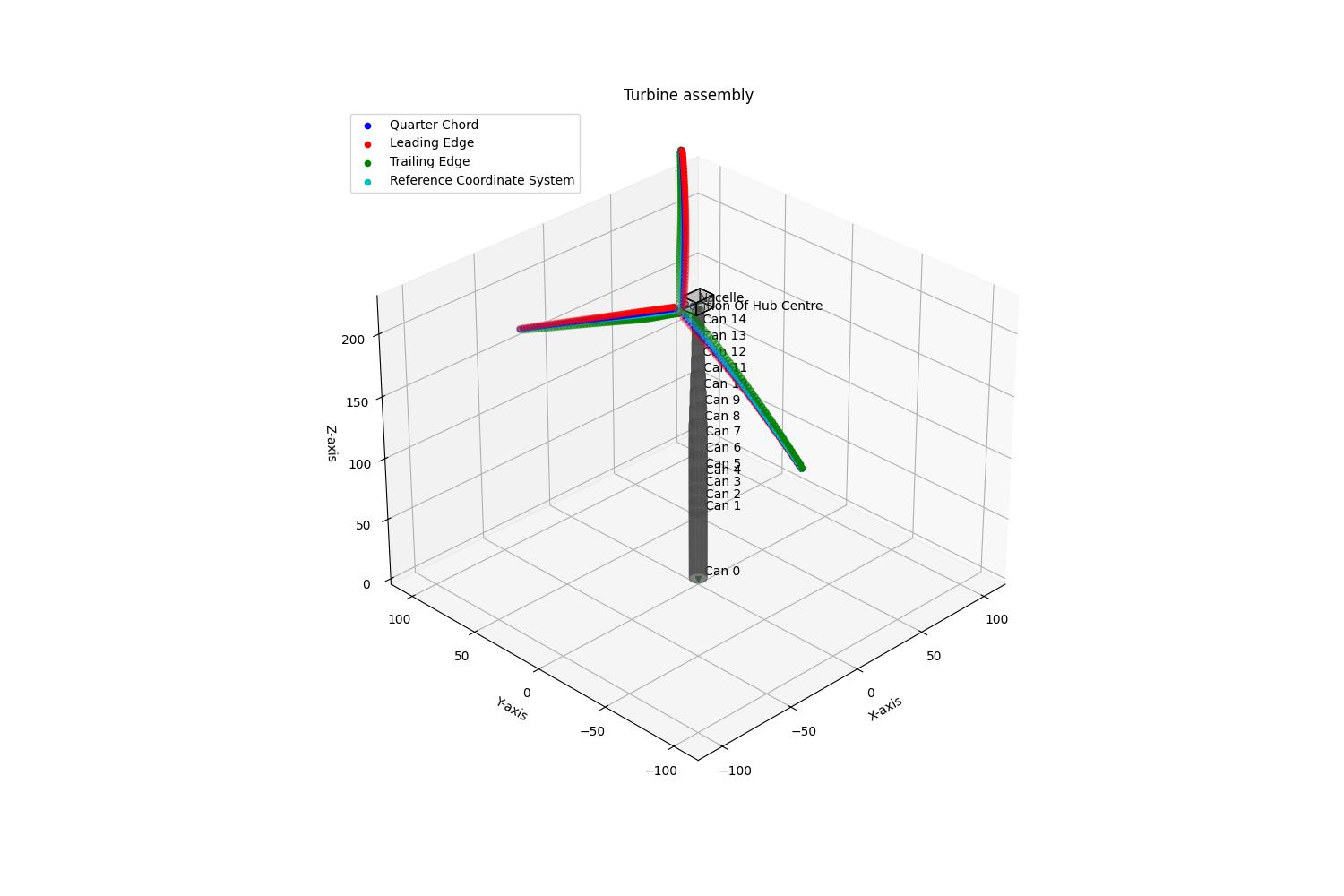
figure_axis.set_title("Turbine assembly")
figure_axis.view_init(elev=30, azim=225) # Change the viewing angle
# Utilising the tree-like structure of the Bladed Next Gen turbine assembly to plot the Tower and output the assembly node position for the DrivetrainAndNacelle
assembly_node = plot_tower(figure_axis, Components['IEA15Tower'])
# Plot the Nacelle and outputs the assembly node position for the Hub
assembly_node, rotor_tilt = plot_nacelle(figure_axis, Components['IEA15DrivetrainAndNacelle'], assembly_node)
# Plot the Hub and outputs the blade mounting points and mounting angles
blade_starting_points, blade_rotations = plot_hub(figure_axis, Components['IEA15Hub'], rotor_tilt, assembly_node)
# Plot the Blades
for i, blade_start_point in enumerate(blade_starting_points):
plot_blade(figure_axis, Components['IEA15Blade'], blade_start_point, blade_rotations=blade_rotations[i])
# Only show the legends for the blade AxesAndCoordinateSystems
handles, labels = plt.gca().get_legend_handles_labels()
plt.legend(handles[:4], labels[:4], loc = 'upper left')
plt.show()